Many attrition models represent armed combat as two uninterrupted streams of fire between the opposing sides – that is, both forces are assumed to be causing and suffering casualties every instant of the engagement.
This allows the analyst to study casualty rates over arbitrarily small increments of time. We refer to these models as continuous or differential models (for their use of differential equations) and the original formulations by Lanchester and Chase, as most of their later revisions by other authors, belong in this category.
Of course, no real exchange of fire is truly “continuous” in the strict sense. One can reasonably expect pauses and changes of pace to exist, and there is no such thing as a fractional bullet or shell to begin with. In this apparent shortcoming, differential combat models showcase an important characteristic of mathematical models in general: the focus is placed on relevance, rather than on realism. We know that discontinuity may exist, but we choose to neglect it when we know that it will not affect our analysis in any significant way.
This assumption can be reasonable in some scenarios, such as prolonged fighting over many days (Engel’s analysis of Iwo Jima, or MacKay’s for the Battle of Britain) or engagements in which large volumes of fire are exchanged with relatively little pause (Lanchester’s own study of the Battle of Trafalgar). In these conditions, even if modelling does not always manage to yield a reasonable fit to reality, it can at least provide some valuable insight on the relationships between the input parameters – and sometimes that is plenty enough. In the words of Clausewitz:
“If theory investigates the subjects which constitute war; if it separates more distinctly that which at first sight seems amalgamated; if it explains fully the properties of the means; if it shows their probable effects; if it makes evident the nature of objects; if it brings to bear all over the field of war the light of essentially critical investigation,—then it has fulfilled the chief duties of its province.”
DISCRETE EVENTS
There are some scenarios, however, in which discontinuity is far from irrelevant.
Advances in military technology throughout the 20th century, particularly in the realm of naval warfare, allow combatants to deliver great amounts of firepower in very short time frames. Torpedo spreads, carrier strikes, and missile salvos deal damage suddenly and violently, often deciding the outcome of a battle in one or two swift blows – a ship might be fully operational one instant, and out of action the next.
This increased punctual lethality of weapon systems, combined with greater ranges of engagement, have turned naval warfare into a mostly discrete (rather than continuous) reality: whatever the duration of a battle might be, the actual exchange of fire is reduced to a few short and clearly separated instances in which vast amounts of damage are dealt. An immediate implication is that one side may surprise the enemy, hitting them before they are able to react – in contrast to gunnery duels, in which unanswered fire is rare.
In these circumstances, time-continuous modelling simply does not cut it, as its theoretical framework is too far removed from the nature of reality. A new approach is necessary.
THE SALVO MODEL
In his 1986 classic Fleet Tactics: Theory and Practice, USN captain Wayne P. Hughes Jr. explores the nature of pulsed combat, beginning with a simple mental exercise on the nature of carrier actions in the Second World War. Hughes begins with the reasonable assumption (somewhat justified by historical data) that one carrier air wing or CVW (known as “Carrier Air Groups” until 1963) could sink or cripple, on average, one enemy carrier in a single sortie.
In what he refers to as a “very rudimentary table”, Hughes shows the expected outcomes of a surprise strike of a force B on a force A, after which any survivors from A are allowed to counterattack:
| Initial Force (A/B) | 2/2 | 4/3 | 3/2 | 2/1 | 3/1 |
| Survivors (A/B) | 0/2 | 1/2 | 1/1 | 1/0 | 2/0 |
In the next few pages of the chapter, this simple rule of thumb is applied to a series of carrier battles of 1942 (The Coral Sea, Midway, Eastern Solomons, Santa Cruz Islands, and the Philippine Sea) obtaining a surprisingly good fit. Later on, the model is slightly altered to account for the effect of defending fighters, which would reduce the striking power of attacking bombers by shooting down or disrupting their formations. In essence:
![]()
This elementary theoretical tool serves as the foundation for a model of modern combat between missile-equipped warships – very similar in many aspects to carrier actions. In such scenarios, anti-ship cruise missiles (ASCMs) take the place of bomber formations, and point defence systems and SAM batteries fill in for defending fighter patrols, but the process remains much the same:
- The attacking side launches a number of missiles at detected enemy elements from beyond visual range.
- The defender attempts to intercept or distract as many of the incoming ASCMs as possible.
- A fraction of the missiles overwhelm the defences or otherwise leak through them, and hit their intended targets, which suffer damage until a threshold is reached and they are rendered out of action.
In a later paper in 1995, titled A salvo model of warships in missile combat used to evaluate their staying power, Hughes constructs the analytical skeleton for this model as follows:
ASSUMPTIONS
Two sides (let us call them Blue and Red) are each made up of identical missile-armed warships. We use the letter A to represent the force strength (in number of warships) of the Blue side, and B for that of the Red side.
Each individual warship has a fighting or striking power, reflecting how many well-aimed missiles it can fire in one salvo. This is α for Blue ships, and β for Red ships.
Warships also have a defensive power, being the number of missiles they can shoot down from an incoming barrage. For consistency with Hughes’ work, we will call this a3 for each ship in the Blue side, and b3 for the Red side.
Finally, warships are also defined by their staying power (a concept previously explored by J.V. Chase in his classified paper of 1902) being the number of hits they can take before being rendered out of action. This we call a1 for Blue ships, and b1 for Red ships.
This established, the process of an attack by A on force B would go like this:
- All ships of force A fire at the enemy, with all their good shots grouped into one large salvo.
- All ships of force B collectively fire their defensive SAMs at the incoming salvo, shooting down some of the incoming missiles.
- The remaining missiles hit force B and distribute their damage uniformly among all available targets.
- It is important to note that both striking and defensive firepower are, in Hughes’ original formulation, dependent on a ship’s status: an undamaged ship will always enjoy its nominal values, but as it suffers hits, its offensive and defensive capabilities will be proportionally reduced.
Depending on the scenario we wish to explore, A and B can attack each other simultaneously, or one can surprise the other. Either situation can happen an arbitrary number of times or until one side is wiped out.
BASIC EQUATIONS
The mathematical equations describing this process are known as the Basic Salvo Equations:
![]()
![]()
An example engagement using this basic formulation is offered in McGunnigle (1999) Appendix A, p.71, with the following input data:
| Blue | Red | |
|---|---|---|
| Units | 3 | 6 |
| Striking pwr. | 3 | 1 |
| Defensive pwr. | 2 | 1 |
| Staying pwr. | 2 | 1 |
And these results plotted per time pulse (salvo):
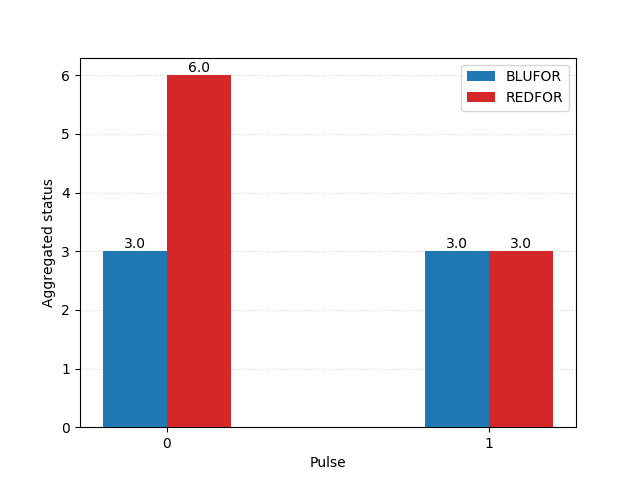
In this example case, the Blue side can fire nine missiles (three per ship) and intercept six, whereas Red can fire six missiles (one per ship) and intercept another six. Blue, then, can intercept all of Red’s ASCMs and survives the salvo unharmed. Red is predictably not so fortunate, as three of Blue’s missiles overwhelm its defences and knock three ships out.
EMBELLISHED MODEL
The model is further developed by many authors, the first being Hughes himself, to account for other possible factors. The additions are often in the form of fractional coefficients (values from 0 to 1) reducing the original parameters to reflect various realities of naval combat. Some examples would be:
- Scouting – affecting total striking power, and representing the fraction of the enemy that a side can actually engage based on sensor range or precision, off-board scouting assets, etc. For instance, a side with a scouting coefficient of ‘0.5’ would only be able to engage one half of the enemy fleet successfully, so its striking power would be reduced by 50%.
- Defensive alertness – like scouting, but affecting defensive firepower instead. Used to reflect how prepared a group is to successfully fend off an attack.
- Training – affecting both striking and defensive power.
- Weapon reliability and accuracy – affecting the probability that shots (offensive or defensive) will hit, to reflect imperfect guidance or firing solutions, manufacturing flaws, etc.
Jeffrey R. Cares provides a variety of scenarios between Knox-class frigates using this kind of embellished model, and data gathered from NAVTAG exercises, in his 1990 paper The fundamentals of salvo warfare. Here is one such encounter taken from page 23 (Scen. VI):
| Blue | Red | |
|---|---|---|
| Units | 2 | 3 |
| Striking pwr. | 4 | 4 |
| Defensive pwr. | 4 | 4 |
| Staying pwr. | 2 | 2 |
| Scouting | 1 | 1 |
Cruise missiles in the model are assigned an accuracy of 0.61 (roughly three fifths are expected to hit) while defences are given an effectiveness of 0.35. These numbers are obtained from the results of the NAVTAG simulation.
The engagement, plotted in our own Python implementation:
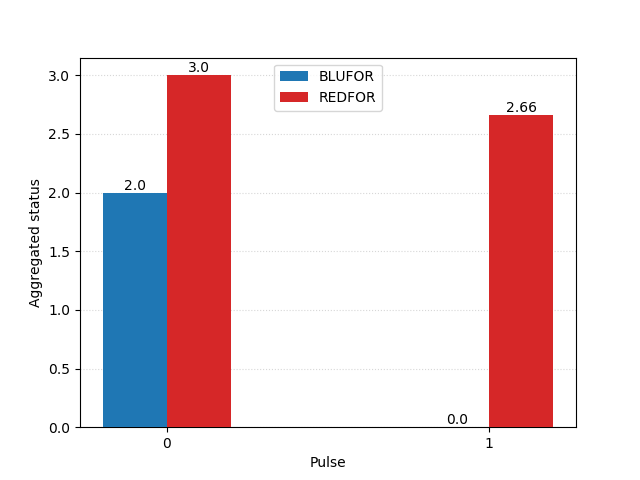
This scenario showcases the importance of concentration of force, in a way that is somewhat reminiscent of Lanchester’s Square Law: with a local numerical superiority of one ship (50% advantage) REDFOR manages to disable all of BLUFOR’s ships, losing none of their own.
Other revisions to the model have been proposed, such as reworking defensive firepower calculations to account for ‘leakers’ – the (hopefully for the defender) small fraction of missiles that are expected to always bypass protective systems , due to the practically limited reliability of chaff and flares, point defence weapons, etc. Yao Ming Tiah (2007) provides a thorough evaluation of scenarios following this rule, of which we detail one (excursion A3, pp. 26 – 29):
| Blue | Red | |
|---|---|---|
| Units | 4 | 12 |
| Striking pwr. | 8 | 4 |
| Defensive pwr. | 6 | 2 |
| Staying pwr. | 1.5 | 1 |
| Scouting | 0.6 | 0.6 |
Tiah assigns missiles a launch reliability of 0.9 (one in ten fails to launch) and an accuracy of 0.7. Defences have an aggregated effectiveness of 0.68. Blufor surpises Redfor and attacks first.
Here is the corresponding plot obtained from our implementation:
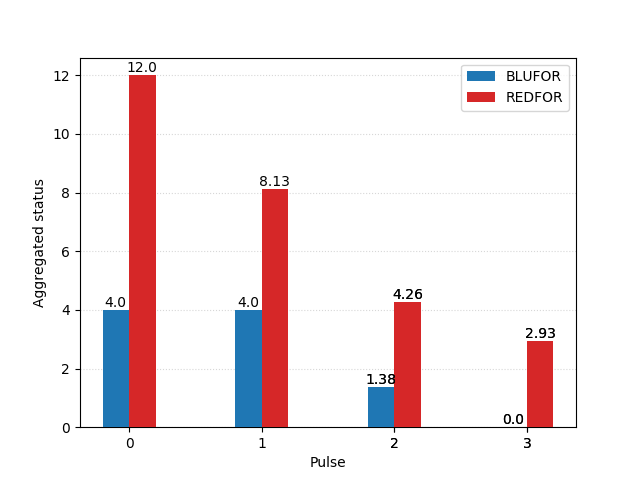
Though ultimately losing the engagement, the heavily outnumbered BLUFOR manage to put just under four of REDFOR’s ships out of action in their surprise attack – almost enough to level the playing field.
STOCHASTIC MODEL AND SIMULATION
All variants of the Salvo model included here are deterministic: given the same input data, they will always produce the same output. As is the case with all deterministic models of combat, the result is meant to be the average expected outcome, not an infallible prediction. War is a chaotic affair by nature, and the purpose of modelling is finding out what can reasonably be expected, rather than a monolithic truth.
However, we might also be interested in the variance (how much can we expect reality to differ from our prediction?) and the distribution (what is the relative probability of a given outcome?) of the possible results.
In this spirit, Armstrong (2004) develops a stochastic version of Hughes’ model, in which some of the parameters are introduced as mean values with a known variance, rather than being fixed. He and Powell use this approach in a 2005 paper to model possible outcomes of the Battle of the Coral Sea.
Another option (used earlier by McGunnigle and Lucas in 2003) is simulation: one or more events (say, a missile hitting its target, or an enemy ship being detected by sensors) are assigned a probability, be it from past combat experience, weapon specifications, or data gathered from tactical exercises. This done, we resolve one instance of the engagement, determining whether these events do happen by using a random process of our choice – today we would use a pseudo-random number generator on a computer, but suffice it to say we are doing a sophisticated roll of the dice, as if we were playing a board game. We then repeat the operation a few thousand times, recording the results for each instance. All that is left is mapping how many times each of the possible outcomes have occurred.
Whichever approach we choose, the result will be similar: instead of an estimated mean prediction (as with the deterministic model) we will obtain a probability distribution of the possible outcomes, which might prove much more valuable for our analysis – especially if our objective is assessing risk.
An additional perk of the stochastic variant is that the need to apply damage uniformly is lifted: missiles can be assigned randomly or semi-randomly to targets using whatever distribution best fits our purposes. As a notable example, Kevin G. Haug published a paper in 2004 in which he experimented with the application of a Pólya urn distribution to missile targeting in the salvo model.
CONCLUSIONS
Elegant and powerful in its simplicity, the salvo model offers a solid foundation for understanding the relationships between various factors in modern naval combat. Hughes himself highlights a few of his own conclusions in the original 1995 paper:
- Superiority in numbers provides a reliable advantage on its own: if side A’s ships have twice the striking power, defensive power, and staying power as side B’s, B can still achieve parity by having twice as many ships as A. Refer to the scenario shown from Cares (1990) earlier in this article.
- Of all parameters taken into account, staying power (the ability of a ship to sustain damage) is the only one that is unaffected by poor tactical choices.
- As J.V. Chase pointed out, staying power does not scale linearly with ship displacement: a ship twice as large is not necessarily twice as hardy. Striking and defensive power can be increased more easily and cheaply, which leads to modern fleets having large destructive potential relative to their ability to sustain damage.
- This causes ‘tactical instability’: small changes in the engagement can lead to grossly different outcomes. A single missile hitting or missing might mark the difference between victory and defeat, as that is often enough to cripple one target entirely.
- In such unstable situations, scouting – the ability to detect the enemy and strike first – becomes paramount. Even a superior fleet must strive whenever possible to land the first blow, as a single salvo from a comparatively inferior opponent is potentially disastrous. The scenario taken from Yao Ming Tiah’s (2007) illustrates this principle.
GitHub
The Python implementations of the models used in this article for plotting simulated combat results can be found in the author’s GitHub page.
FURTHER READING
- Hughes, Wayne P., Jr. – A Salvo Model of Warships in Missile Combat Used to Evaluate Their Staying Power (1995)
- Cares, J.R. – The Fundamentals of Salvo Warfare (1990)
- McGunnigle, John – An exploratory analysis of the military value of information and force (1999)
- Armstrong, Michael J – A stochastic salvo model for naval surface combat (2004)
- Haugh, Kevin G. – Using Hughes’ Salvo model to examine ship characteristics in surface warfare (2004)
- Tiah, Yao Ming – An analysis of small navy tactics using a modified Hughes’ salvo model (2007)
